templated modular arithmetic, modulo a prime \(p\) More...
#include <modp.hpp>
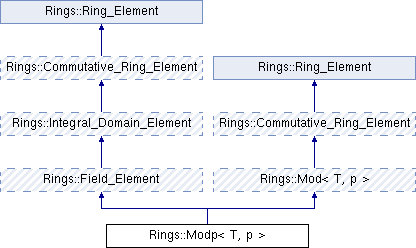
Inheritance diagram for Rings::Modp< T, p >:
Public Member Functions | |
| Modp () | |
| initializes to zero | |
| Modp (T) | |
| initializes to given value | |
| Modp (const Mod< T, p > &other) | |
| copy constructor of parent type (should be safe, thanks to modulus) | |
| Modp (const Modp< T, p > &other) | |
| copy constructor of same type | |
| virtual Modp< T, p > & | operator* (const T &other) const override |
| multiplication of value with element of base type | |
| virtual Modp< T, p > & | operator/ (const Field_Element &other) const override |
| division: other element should be of same type, use a cast | |
| virtual Modp< T, p > & | inverse () const override |
| multiplicative inverse | |
| virtual bool | has_inverse () const override |
| fields are integral domains where nonzero elements have inverses | |
 Public Member Functions inherited from Rings::Integral_Domain_Element | |
| virtual bool | is_cancellable () const override |
| integral domains are commutative rings without zero divisors, so the element should be cancellable (see description of class) | |
| Public Member Functions inherited from Rings::Commutative_Ring_Element | |
| virtual bool | is_commutative () const override |
| Duh. | |
| Public Member Functions inherited from Rings::Mod< T, p > | |
| Mod () | |
| initializes to 0 | |
| Mod (T v) | |
| initializes to give value | |
| Mod (const Mod< T, m > &other) | |
| copy constructor | |
| virtual bool | is_one () const override |
True iff assigned value is congruent to 1 | |
| virtual bool | is_zero () const override |
True iff assigned value is congruent to 0 | |
| virtual Mod< T, m > & | operator+ (const Ring_Element &other) const override |
| implements modular addition | |
| virtual Mod< T, m > & | operator- (const Ring_Element &other) const override |
| implements modular subtraction | |
| virtual Mod< T, m > & | operator* (const Ring_Element &other) const override |
| implements modular multiplication | |
| const Mod< T, m > & | operator= (const Ring_Element &) |
| assignment operator may be needed | |
| virtual bool | operator== (const Ring_Element &) const override |
| comparison: other element has same value | |
| virtual bool | operator!= (const Ring_Element &) const override |
| comparison: other element has different value | |
| T | get_value () const |
| returns value of this modulus | |
Protected Member Functions | |
| virtual void | check_inverse () noexcept override |
redefines Mod’s check_inverse() to do nothing | |
| void | check_inverses () |
| checks whether inverse are set up, and if not sets them up | |
| Protected Member Functions inherited from Rings::Mod< T, p > | |
| void | adjust_value () |
| ensures value is at least 0 but less than modulus | |
| void | check_modulus () |
| checks modulus to ensure we aren't trying to do the impossible More... | |
Static Protected Attributes | |
| static vector< T > | inverses |
| lists inverses for all nonzero elements | |
Related Functions | |
(Note that these are not member functions.) | |
| template<typename T , T p> | |
| constexpr Modp< T, p > | initialize_inverses |
| used to force an initialization of inverses at compilation | |
| Related Functions inherited from Rings::Mod< T, p > | |
| constexpr Mod< T, m > | prevent_zero_modulus |
| used to prevent the use of a zero modulus | |
| ostream & | operator<< (ostream &os, const Mod< T, m > &x) |
| prints only value, not the modulus | |
Additional Inherited Members | |
| Protected Attributes inherited from Rings::Mod< T, p > | |
| T | value |
| value of the element | |
| bool | invertible |
| whether the element is invertible | |
Detailed Description
template<typename T, T p>
class Rings::Modp< T, p >
templated modular arithmetic, modulo a prime \(p\)
The first template value indicates the base type (e.g., int, long). This code assumes you’re working with something int -like so no guarantees if you try something else. The second template indicates the modulus, which should be a prime number. This guarantees inverses for every nonzero element of the field, but see the warning.
- Warning
- If the modulus is nonzero then you get what you’re asking for!
- Examples:
- test_polynomial.cpp, and test_rings.cpp.
The documentation for this class was generated from the following file:
