elements of this type should be cancellable; there should be no zero divisors More...
#include <rings.hpp>
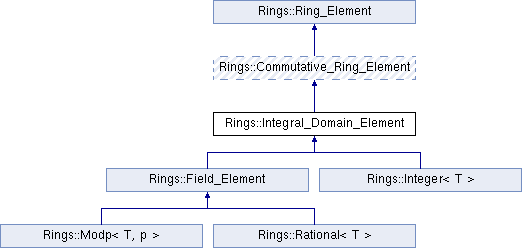
Inheritance diagram for Rings::Integral_Domain_Element:
Public Member Functions | |
| virtual bool | is_cancellable () const override |
| integral domains are commutative rings without zero divisors, so the element should be cancellable (see description of class) | |
 Public Member Functions inherited from Rings::Commutative_Ring_Element | |
| virtual bool | is_commutative () const override |
| Duh. | |
| Public Member Functions inherited from Rings::Ring_Element | |
| virtual bool | is_one () const =0 |
should be True iff element is multiplicative identity | |
| virtual bool | is_zero () const =0 |
should be True iff element is additive identity | |
| virtual bool | has_inverse () const =0 |
should be True iff element has a multiplicative inverse | |
| virtual bool | operator== (const Ring_Element &) const =0 |
| comparison: other element has same value | |
| virtual bool | operator!= (const Ring_Element &) const =0 |
| comparison: other element has different value | |
| virtual const Ring_Element & | operator+ (const Ring_Element &) const =0 |
| addition: other element should be of same type, use a cast | |
| virtual const Ring_Element & | operator- (const Ring_Element &) const =0 |
| subtraction: other element should be of same type, use a cast | |
| virtual const Ring_Element & | operator* (const Ring_Element &) const =0 |
| multiplicationL other element should be of same type, use a cast | |
Detailed Description
elements of this type should be cancellable; there should be no zero divisors
Zero divisors are any \(a,b\neq0\) such that \(ab=0\). By “cancellable” we mean the following: \(ax=ay\Rightarrow a(x-y)=0\), so if \(a\neq0\) then \(x-y=0\Rightarrow x=y\); that is, we cancelled.
The documentation for this class was generated from the following file:
